L’utilisation de plusieurs méthodes d’estimation des incertitudes de mesurage est-elle un choix ou une obligation ?
C’est pour cela que le niveau de risque accepté pour nos mesurages, essais, analyses a pris une importance majeure et un autre chemin de réflexion vers la recherche de moyens et d’outils de validation de nos résultats.
Généralement, la détermination des incertitudes s’effectue avec la méthode GUM (Guide to the expression of uncertainty in measurement) [JCGM 100:2008] basée sur la méthode de propagation des variances appelée par les métrologues « méthode de propagation des incertitudes ». Ce guide a été complété par le Supplément 1 [JCGM 101:2008] du guide pour l’expression des incertitudes de mesure de 2008 traitant la propagation de distributions par la méthode Monte Carlo, une alternative pratique du GUM lorsque la méthode de propagation des variances n’est pas facilement applicable.
L’application de ce Supplément 1 du GUM basé sur une méthode de simulation Monte Carlo développée pour la résolution des modèles complexes. Une méthode statistique révolutionnaire été utilisée pour la première fois en 1947 par Nicholas Metropolis afin de résoudre un besoin d’étude des probabilités de gain des jeux au hasard pour le Casino de Monte Carlo. Celle-ci est basée sur des simulations statistiques des probabilités de distributions des facteurs d’entrée.
Traitons l’exemple S7 décrit dans le document EA-4/2 :2021 concernant l’étalonnage d’un atténuateur de pas coaxial à un réglage de 30 dB en utilisant le logiciel Gum Workbench 2.4 pour l’application des deux méthodes GUM et la méthode de simulation Monte Carlo.
Le modèle mathématique Lx relatif à l’atténuateur à étalonner tel que décrit dans l’exemple EA-4/2 :2021 est :
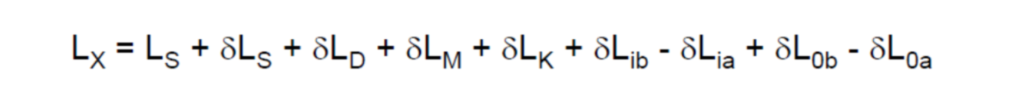
Lx résultat de l’atténuation de l’atténuateur à étalonner en dB qui représente notre mesurande et les facteurs LS, δ LS, δ LD, δ LM, δ LK , δ Lib , δ Lia , δ L0b et δ L0a représentent les différents facteurs d’entrées du modèle mathématique (formule N°1)
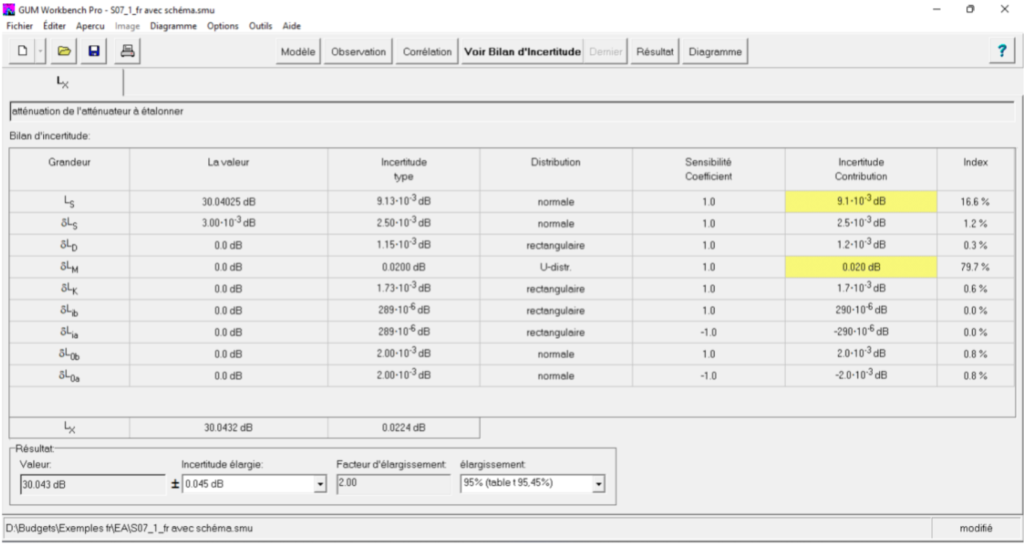
Extrait du logiciel GUM Workbench 2.4
Le bilan d’incertitude présenté par la figure N° 1 met l’accent sur un paramètre prépondérant qui est la correction due à une perte de concordance δ LM , celle-ci représente 79,7% de la valeur de l’incertitude globale qui a été estimé par la distribution arc-sinus.
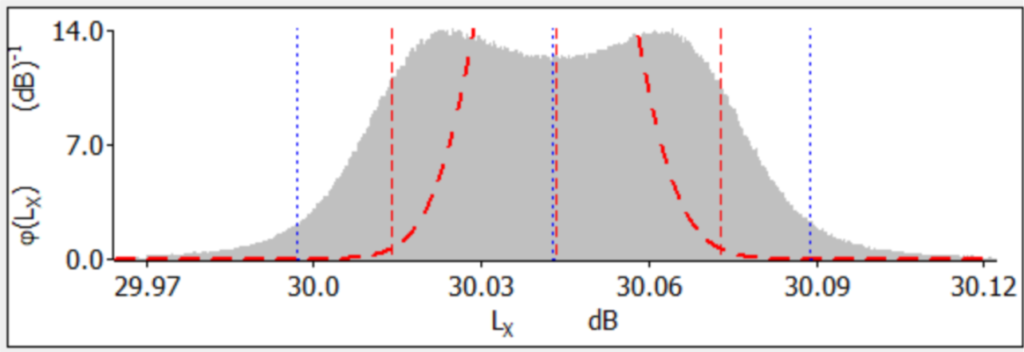
Le résultat de la simulation d’une population de 2 millions d’essais, effectuée par des blocs de 10 000 essais est présenté par la figure N°2 de cet article.
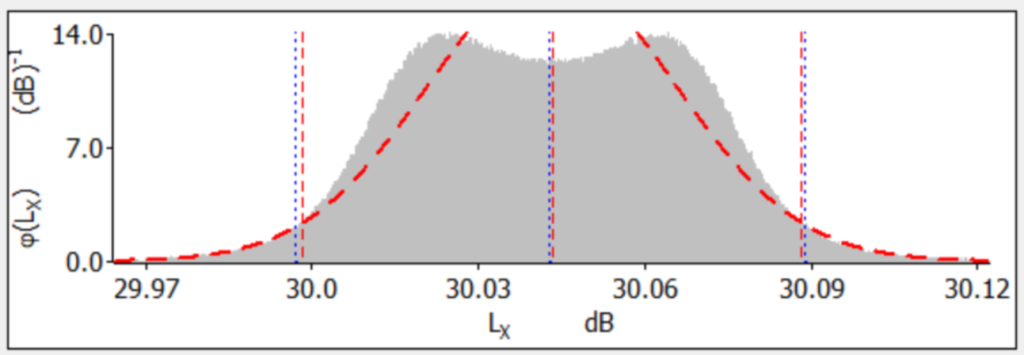
GUM Workbench 2.4, Simulateur OMCE V:1.2.14.1
Les résultats de simulation du modèle mathématique de l’équation N° 1 sont présentés en couleur gris et les valeurs théoriques attendues sont schématisées en couleur rouge, les traits bleus représentent le calcul basé sur des données expérimentales.
Malgré que la courbe de simulation du modèle n’est pas ce qu’on attendait, une courbe de distribution normale, le niveau d’incertitude donné est rassurant et représente une probabilité de 4,6%, un niveau de risque accepté par les métrologues. La question, si on change la distribution de ce paramètre, est de savoir quel est l’impact sur le niveau de risque pris.
GUM Workbench 2.4, Simulateur OMCE V:1.2.14.1
Observons l’impact sur un choix non adapté, la loi de distribution du paramètre δ LM a été changée de la loi arc sinus vers la loi triangulaire, donc d’une probabilité qui tend vers l’infini aux deux extrémités de variation du facteur δ LM vers une probabilité maximale vers le centre du facteur en question. Le résultat est très représentatif, il relève un écart important entre les résultats expérimentaux simulés et les résultats théoriques de la formule du mesurande, avec un risque sur la détermination de résultat proche de 40%, risque non accepté par les utilisateurs du résultat de mesurage.
Aurions-nous perçu cette problématique si on ne procède pas à une détermination des résultats de mesurage par les deux méthodes GUM et Monte Carlo ?
Plusieurs exemples pratiques démontrent l’importance de la comparaison entre les deux méthodes pour la validation adéquate de nos méthodes d’estimation des incertitudes et la détermination de nos résultats de mesurage.
Avec :
- LX : atténuation de l’atténuateur à étalonner (en dB)
- LS =Lib – Lia : différence de l’atténuateur de référence entre 30 dB et 0 dB (en dB)
- δ LS : correction obtenue à partir de l’étalonnage de l’atténuateur de référence (en dB)
- δ LD : correction due à la dérive de l’atténuateur de référence au cours du temps (en dB)
- δ LM : correction due à une perte de concordance (en dB)
- δ LK : correction des signaux de fuite entre l’entrée et la sortie de l’atténuateur à étalonner en raison d’une isolation imparfaite (en dB)
- δ Lib : correction due à la résolution limitée du détecteur de référence à 30 dB (en dB)
- δ Lia : correction due à la résolution limitée du détecteur de référence à 0 dB (en dB)
- δ L0b : correction due à la résolution limitée du détecteur de zéro à 30 dB (en dB)
- δ L0a : correction due à la résolution limitée du détecteur de zéro à 0 dB (en dB)
Pour plus d’informations, rendez-vous sur aequoltd.com
Par :
Mona MAKHLOUF NAFATI
Représentante de Metrodata GmbH
CEO & Co-fondatrice Aequo Ltd
+00 33 (0)6 67 66 78 91 (France)
mona.makhlouf@aequoltd.com
dB Vib – Une première au Global Industrie de Paris !
dB Vib Instrumentation participera pour la première fois au salon Global Industrie 2026 à Paris, événement de référence dédié aux solutions industrielles. Pour cette occasion, dB Vib Instrumentation présentera une sélection de solutions de mesure et de diagnostic, incluant des caméras infrarouges pour la thermographie industrielle, des systèmes d’alignement laser, ainsi que des équipements dédiés […]
VigiSensys : quand la mesure devient un levier de performance
La mesure évolue. Vos exigences aussi. En 2026, VigiTemp devient VigiSensys et affirme une ambition claire : accompagner les laboratoires de tous les secteurs (dont l’industrie) vers une métrologie plus intelligente, plus fluide et plus performante. À l’occasion de Global Industrie 2026, MC2 lève le voile sur sa nouvelle génération de sondes et son logiciel […]
Environnements extrêmes : Metravib Engineering conjugue simulation et essais pour protéger les technologies critiques
Dans des secteurs de pointe tels que l’aérospatiale, la défense ou l’énergie, la survie des équipements sensibles ne tient souvent qu’à un fil — ou plutôt, à la qualité de leur protection mécanique. Face à des environnements de plus en plus hostiles, Metravib Engineering, expert reconnu en ingénierie vibratoire, déploie des solutions d’atténuation sur mesure […]




